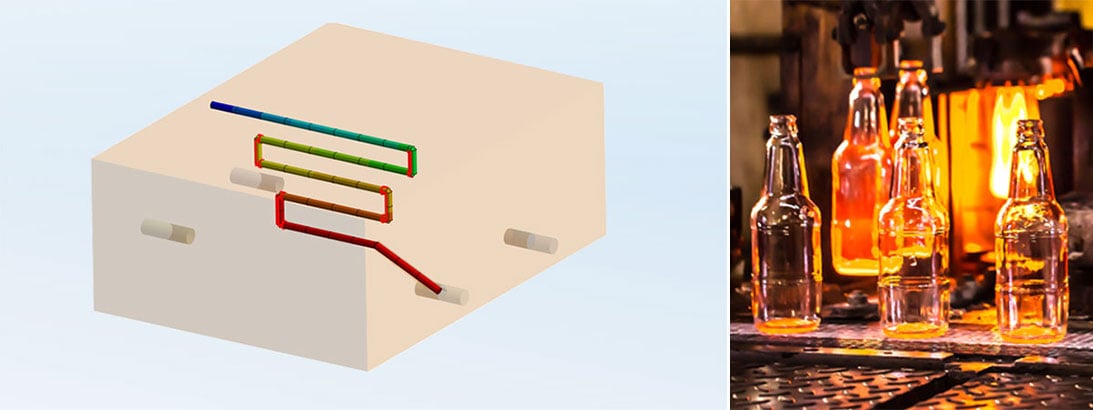
Un processus en cours avec G(l)as

Vous l'avez peut-être posé à côté de vous sur la table : Une bouteille en verre contenant une boisson. Ce verre, qui empêche votre boisson de se répandre sur toute la table, était autrefois produit dans une verrerie. Pour ce faire, des matières premières appropriées (par exemple du sable de quartz) ou des morceaux de verre provenant de conteneurs de verre usagé sont portés à des températures très élevées au-dessus du point de fusion et finalement fondus en une masse homogène. De petites portions de cette masse fondue sont placées dans des moules où elles prennent leur forme finale et sont refroidies à température ambiante.

L'électricité peut-elle remplacer le gaz ?

Une possibilité de chauffage très efficace dans les processus de fabrication est offerte par la mise à disposition de puissance électrique ou électromagnétique. Dans ce cas, les puissances peuvent être appliquées de manière très ciblée et sans grandes pertes thermiques dans la pièce à chauffer. Dans l'industrie de transformation des métaux en particulier, de tels processus se sont déjà assurés leur part et se répandent en outre peu à peu.

Par rapport aux métaux, le verre présente un inconvénient non négligeable : à température ambiante, la conductivité électrique du verre est si faible qu'un réchauffement par des sources électriques et électromagnétiques ne fonctionne pas. Toutefois, à partir d'une température élevée d'environ 1000°C, le verre devient un conducteur d'ions. La conductivité électrique reste donc nettement inférieure à celle des métaux, mais cela suffit pour garantir un flux de courant électrique et donc, en fin de compte, pour convertir directement la chaleur dans le verre par le biais de la puissance électrique.

La réponse claire à la question "L'électricité peut-elle remplacer le gaz ? Non, il faut toujours un processus de démarrage, qui est réalisé par une flamme de gaz. Dès qu'un courant électrique est établi, le processus PEUT en principe être conduit uniquement avec de l'énergie électrique : Les nouveaux matériaux froids sont fondus par conduction thermique et si le processus peut être conduit en continu, cela serait théoriquement envisageable. Mais il y a encore des choses comme la "maintenance", le "changement de lot", les "pannes", etc. qui viennent perturber le bon fonctionnement du monde électrique.

Est-il possible de passer du gaz à l'électricité ? | © Adobe Stock 

Électrique ou non électrique...

... c'est peut-être la question qui convient ici. Si vous modifiez le lieu et le type d'apport de puissance dans votre processus, la répartition de la température change naturellement aussi et cette répartition de la température est finalement déterminante pour le processus. Toutefois, la question se pose de savoir COMMENT la répartition de la température change.Text section 2 (max. 3 paragraphs with max 720 characters each):

Il est toutefois difficile d'effectuer des mesures à l'aide de thermocouples et/ou d'appareils de mesure de flux, en particulier dans le cas de verres en fusion très agressifs. Pour analyser dans quelle mesure le profil de température et donc le processus se comportent en cas de modification de l'apport de puissance, la simulation numérique est toutefois appropriée. Elle permet d'évaluer les grandeurs scalaires et vectorielles en tout lieu et à tout moment, et ce même sans l'influence que pourrait avoir l'introduction d'un instrument de mesure. De plus, l'électricité et la température s'influencent mutuellement, c'est pourquoi la simulation doit être réalisée de manière couplée afin de générer des résultats utilisables.

© Adobe Stock

Électrique ou thermique ? Non, les deux !

Le processus mentionné ici comprend donc à la fois des effets électriques et thermiques, qui s'influencent en outre mutuellement. Le flux de chaleur provenant d'une flamme de gaz, associé aux pertes électriques de l'alimentation électrique, détermine le champ de température. Pour répondre à toutes ces exigences, Ansys propose le système "Coupled Field" avec les conditions limites et les charges

Possibilités d'un système de champs couplés | © CADFEM Germany GmbH

D'ailleurs, par rapport au système "Thermal Electric", les systèmes "Coupled-Field" offrent en plus la prise en compte d'un transport de masse... ou l'analyse d'effets mécaniques... ou la prise en compte de phénomènes acoustiques. Il suffit de sélectionner dans la région Physics les domaines de sa propre liste de souhaits et c'est parti !

A propos de couplage : Au sein de la simulation, on distingue le couplage faible et le couplage fort ou matriciel. Dans le cas d'un couplage faible, les sous-disciplines travaillent de manière séquentielle. Dans notre exemple, la matrice électrique serait d'abord résolue et la densité de puissance dissipée évaluée. Cette densité de puissance serait ensuite la grandeur d'entrée pour le calcul thermique. Le champ thermique serait calculé et renvoyé au système électrique pour l'adaptation des données relatives aux matériaux. Le système "Coupled Field" utilise le couplage fort. Dans le cas d'un couplage fort, les dépendances respectives sont intégrées dans la matrice, c'est pourquoi une solution convergente doit être obtenue SIMULTANEMENT pour les deux sous-disciplines.

Il s'agit donc maintenant de déterminer le meilleur rapport possible entre le chauffage conventionnel et le chauffage électrique, en tenant compte de tous les effets et influences réciproques. Un modèle de démonstrateur permet de réaliser des études qualitatives et de déterminer les relations entre les grandeurs d'entrée (température de la flamme de gaz, débit massique du verre, tension électrique aux électrodes) et de sortie (température au point de coulée, puissance du gaz, puissance électrique).

Le savoir scolaire mis en pratique !

L'apport d'énergie thermique à partir de la flamme du gaz se fait par rayonnement et convection. La troisième partie par conduction peut généralement être négligée. Pour les structures plus complexes, le solveur de rayonnement peut entraîner des temps de calcul trop longs. Un petit conseil : une condition limite de convection dépendant de la température, qui tient compte de la convection "normale" et du rayonnement, permet d'y remédier. Selon la loi de Newton, la densité du flux de chaleur en cas de convection est : q=α∙Δϑ. Dans le cas de la loi de Stefan-Boltzmann, la relation est la suivante, si un échange de rayonnement avec d'autres surfaces peut être négligé :  q=σ∙ε∙(T⁴ - T_U⁴ ) – avec T comme température absolue.

La densité totale du flux de chaleur est la somme des deux mécanismes agissant en parallèle. Si l'on fait maintenant appel à ses connaissances scolaires et que l'on se souvient de la "troisième formule binomiale", on se rend compte que

q=σ∙ε∙(T⁴ - T_U ⁴ )=σ∙ε∙(T² + T_U ²)∙(T² - T_U² )

Si l'on utilise à nouveau ce procédé, on obtient

q=σ∙ε∙(T⁴ - T_U⁴ )=σ∙ε∙(T² + T_U² )∙(T + T_U)∙(T - T_U )

La dernière parenthèse représente ainsi la différence de température, telle qu'elle apparaît également dans la loi de Newton. L'ensemble du facteur qui précède fonctionnerait donc comme un coefficient de convection effectif, dépendant de la température, afin de tenir compte des effets du rayonnement.

Pour notre démonstrateur simple, nous utilisons un flux de chaleur pour décrire la puissance du gaz, un parcours exemplaire du matériau introduit jusqu'au point de coulée et quatre électrodes : Deux à potentiel positif, deux à potentiel nul. Les côtés extérieurs du four sont relativement froids grâce à la bonne isolation thermique, c'est pourquoi une condition de bord de rayonnement n'est pas nécessaire ; ici, seule une condition de bord de convection simple est utilisée, mais elle n'est pas mentionnée dans la figure pour préserver la clarté.

Modèle de simulation avec conditions limites et charges | © CADFEM Germany GmbH

 Analysis gas power - electric power | © CADFEM Germany GmbH 

Images de couverture : Liens : © CADFEM Germany GmbH | Droite : © Adobe Stock
Première publication : Juillet 2023