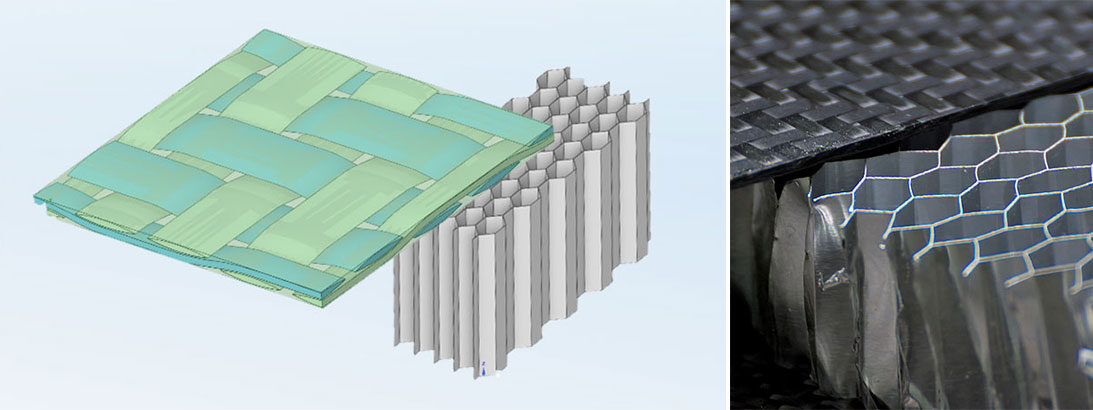
De la microstructure aux paramètres du matériau

Tous les matériaux ont une structure interne, qu'il s'agisse du métal bien connu constitué de ses cristaux ou des polymères complexes avec leurs chaînes moléculaires enchevêtrées. En outre, nous, les ingénieurs, combinons différents matériaux et créons des matériaux composites haute performance en renforçant les particules ou les fibres pour répondre à nos besoins. Que nous puissions voir la structure du matériau ou non, elle définit toutes ses propriétés. Ce serait bien sûr génial si nous pouvions immédiatement déduire des valeurs pour la simulation à partir de la connaissance de la microstructure. Mais ce n'est malheureusement pas si simple, ou savez-vous quelle est la contrainte d'écoulement pour une taille de grain de 10 µm ?

Heureusement, nous n'avons pas besoin de paramètres tels que la taille des grains dans notre analyse d'emboutissage. Cependant, Ansys exige des entrées telles que la courbe de solidification ou les constantes d'orthotropie. Comment obtenir les données nécessaires ? La voie royale est certainement de demander à un physicien doué qui résout le problème avec un calcul intégral virtuose sur la seule base des constantes naturelles. Si l'on n'a pas quelqu'un de ce genre, la voie la plus évidente et malheureusement la plus coûteuse est l'expérimentation : fabriquer et tester des échantillons pour chaque variante de la microstructure. Outre les coûts élevés, la quantité de tests réalisables est malheureusement limitée et les propriétés souhaitées ne peuvent pas être déterminées.

Avec des possibilités mathématiques terrestres et des moyens financiers limités, il existe toutefois une solution : la simulation ! Il est désormais très répandu de créer des modèles FE, appelés éléments volumiques représentatifs (RVE), de la microstructure. L'idée est séduisante : le comportement des différents composants tels que le polyamide et le verre d'un plastique renforcé par des particules peut être déterminé une seule fois à un coût assez faible. Pour répondre à la question de savoir quel est l'effet de 10% ou 30% de billes de verre renforcées, il suffit de simuler à volonté des essais de traction, de compression, de cisaillement dans différentes directions. Ces données de mesure "synthétiques" peuvent être utilisées pour déterminer les propriétés du composite. C'est ce qu'on appelle l'homogénéisation.

De gauche à droite : éléments de volume représentatifs périodiques d'un plastique renforcé à 10 %, 20 % et 30 % de particules | © CADFEM

À quoi ressemble le flux de travail de l'homogénéisation ?

Prenons l'exemple du renforcement des particules pour décrire brièvement les étapes de l'homogénéisation. Le premier point, de loin le plus dur, est la création de la géométrie. Les RVE sont souvent modélisées comme des parallélépipèdes qui représentent une section périodique de matériau. Il faut d'abord répondre à des questions telles que : quelle forme doivent avoir les particules et sont-elles toutes de la même taille ou y a-t-il une fonction de distribution ? Ensuite, les particules doivent être placées sans collision dans le RVE et ce, en tenant compte de la fraction de volume et de la périodicité. Comme certaines particules sont coupées par les bords, des formes géométriques plus complexes apparaissent même pour les sphères.

Une fois la géométrie créée, il faut la mailler. Bien sûr, on aimerait un maillage périodique et cohérent aux interfaces matrice-particules pour éviter les contacts. Ce sont surtout les petits interstices entre les particules qui donnent des maux de tête, car ils créent de petits éléments. Comme un réseau périodique ne produit pas à lui seul un résultat périodique, on applique ce que l'on appelle des conditions limites périodiques. Il s'agit d'équations de couplage entre les nœuds sur les surfaces de coupe opposées. On obtient ainsi que le RVE déformé puisse être aligné de manière exactement périodique. La manière d'éviter les surcontraintes sur les bords du RVE est un casse-tête très apprécié.

Les déformations RVE effectives sont habilement intégrées dans les équations de couplage. Sur un RVE cubique de 1 µm de côté, le vecteur de distance entre deux nœuds couplés dans la direction x est [Δr₀]=[1 0 0] µm. µm. Si l'on veut appliquer un allongement RVE effectif ε_xx de 2% on force un vecteur d'espacement de [Δr]=[1,02 0 0)] µm à l'état déformé. La périodicité s'exprime par le fait que le vecteur distance est le même pour tous les nœuds couplés d'une paire de surfaces. Ces changements d'espacement provoquent des tensions à partir desquelles le tenseur de tension effectif du RVE est déterminé. Celui-ci constitue, avec les allongements effectifs RVE, les données de mesure "synthétiques" pour le calibrage des modèles de matériaux.

Extrait de matériau périodique et principe des conditions limites périodiques à l'état non déformé (à gauche) et à l'état déformé (à droite) | © CADFEM

Le Material Designer d'Ansys

En tant que doctorant à l'université, j'ai mis en œuvre la méthode d'homogénéisation décrite ci-dessus pour divers RVE au moyen de scripts. C'est avec un œil qui rit et un œil qui pleure que, bien plus tard, j'ai ouvert pour la première fois Ansys Material Designer et analysé un RVE renforcé par des fibres courtes. Le fait que l'ensemble du flux de travail soit entièrement automatisé, à commencer par la création de la géométrie, m'a immédiatement enthousiasmé, mais m'a également fait prendre conscience de la durée de vie et des efforts que je devais auparavant investir dans cette partie artisanale. Tout cela fait partie du passé.

Que reste-t-il donc à faire ? Pour la mécanique structurelle, le comportement du matériau des composants individuels tels que la densité, le module d'élasticité et le coefficient de contraction transversale doit être défini dans les données techniques du Material Designer. Il faut bien sûr entrer les paramètres de microstructure déterminants, puis, après quelques réglages d'analyse, on peut déjà commencer. Une fois les calculs terminés, la cellule Material Designer peut être reliée aux données techniques d'une analyse en aval et le matériau homogénéisé peut être utilisé. La carte des matériaux peut également être ajoutée à la base de données ou exportée sous forme de fichier xml, de sorte que l'homogénéisation ne doit être effectuée qu'une seule fois par matériau !

Pour les composites avec des propriétés statistiques, il y a encore une remarque importante : la RVE doit être grande par rapport aux fibres ou aux particules et en contenir beaucoup. En principe, il faut faire une étude concernant la taille de la RVE et la choisir suffisamment grande pour que les propriétés convergent. Cela peut être très coûteux, car un RVE de longueur d'arête double a huit fois plus d'éléments et le temps de calcul augmente de manière disproportionnée avec les degrés de liberté. Le Material Designer offre toutefois une solution : il est possible d'analyser plusieurs RVE pour un jeu de paramètres et de faire la moyenne des résultats. Cet effort n'augmente que linéairement et est donc plus efficace.

Flux de travail des concepteurs de matériaux dans Ansys Workbench | © CADFEM

Exemple : plastique renforcé de particules

Prenons un exemple : Nous voulons renforcer une matrice composée de PA6 avec des particules de verre et le module d'élasticité doit doubler par rapport à la matrice pure. La grande question est : quelle doit être la proportion de particules ? Dans la base de données GRANTA Material Data for Simulation, nous trouvons des propriétés élastiques linéaires : E_PA6= 1100 MPa, ʋ_PA6=0,35 und E_Glas= 7000 MPa, ʋ​​​​​​​_Glas=0,21. Pour simplifier, nous supposons que les particules sont sphériques avec une distribution uniforme du diamètre entre 5 µm et 15 µm. La taille de la RVE est de 30 µm. Les valeurs cibles pour les fractions volumiques de particules analysées sont 10 %, 20 % et 30 %, avec 3 RVE par fraction volumique.

Le tableau ci-dessous résume les résultats. On peut voir que la part de volume n'est pas exactement atteinte et que les résultats présentent une dispersion. Toutefois, compte tenu de la taille des RVE, on pouvait s'y attendre. Ces effets diminuent avec des RVE plus grandes. Comment évaluer maintenant les résultats ? En tant qu'ingénieur, je dois dire que cela suffit ! Étant donné que l'on ne peut de toute façon pas commander un matériau avec 27,3578 % de particules et que les grandeurs d'entrée sont également soumises à des variations, cette précision est tout à fait suffisante. Dans cette mesure, 30 % de fraction volumique suffiraient à doubler le module d'élasticité d'un matériau composite par rapport à la matrice pure, ce qui permettrait de résoudre avec succès cette tâche complexe à peu de frais.

Au-delà de l'élasticité - quelle est la suite ?

Les propriétés linéaires telles que la densité, les propriétés élastiques et thermiques sont déterminées de manière totalement autonome par le concepteur du matériau. Mais qu'en est-il si nous voulons déterminer nous-mêmes le comportement plastique effectif à l'aide de la simulation ? Certes, le Material Designer offre certaines possibilités d'effectuer des analyses non linéaires, mais nous n'obtiendrons une liberté totale que lors du passage à Ansys Mechanical. Un simple lien sur la page du projet nous permet d'importer facilement la géométrie maillée périodique du Material Designer dans Ansys Mechanical. Après avoir appliqué les conditions limites périodiques, il est possible de simuler n'importe quelle situation de charge avec des cycles, des phases d'arrêt et des changements de direction de charge.

Dans l'exemple suivant, le comportement plastique du matériau d'un composite renforcé par des fibres courtes est simulé. La matrice en polyamide est modélisée avec un matériau plastique et une consolidation isotrope, et les fibres de verre sont élastiques. Pour les matériaux anisotropes, on réalise volontiers des essais de traction dans des directions inclinées par rapport à l'orientation des fibres. Cela peut être effectué très facilement dans Ansys Mechanical via "Part Transform". Les courbes de contrainte-déformation simulées montrent une nette influence de la direction et peuvent maintenant être utilisées pour calibrer la plasticité de Hill, tout comme si elles avaient été mesurées lors de l'expérience.

En résumé, Ansys Material Designer est un laboratoire numérique puissant pour les matériaux. En combinaison avec Ansys Mechanical, il n'y a pratiquement pas de limites à l'analyse des propriétés complexes des matériaux, qui ne peuvent pas être déterminées expérimentalement ou seulement à grands frais. Je vous lance donc un appel : essayez vous-même ! Sculptez le matériau qui répond à vos besoins.

Allongement plastique accumulé dans un plastique renforcé de fibres courtes (à gauche) à un allongement effectif de 7 % et courbes contrainte-déformation simulées lors d'essais de traction dans des directions inclinées par rapport à l'orientation des fibres (à droite) | © CADFEM

Images de couverture: Liens :  © CADFEM GmbH | Droite : © Adobe Stock
Première publication : Juillet 2023