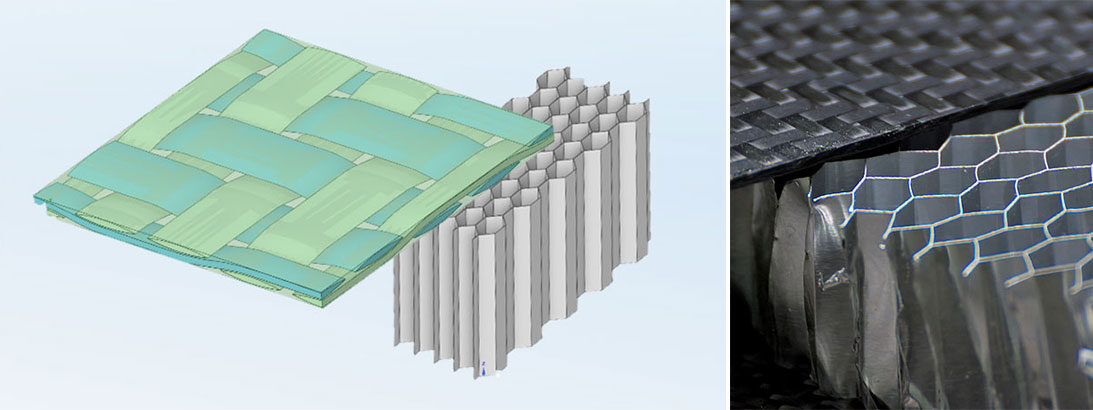
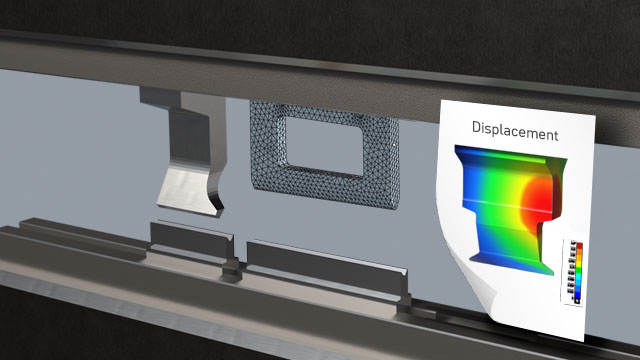
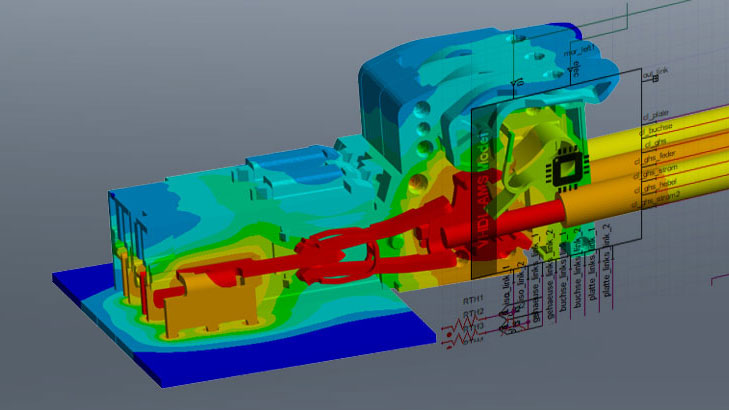
Von der Mikrostruktur zu den Materialparametern

Alle Materialien haben eine innere Struktur: Sei es das wohlbekannte Metall bestehend aus seinen Kristallen oder die komplexen Polymere mit Ihren vernetzten und verschlauften Molekülketten. Darüber hinaus kombinieren wir Ingenieure unterschiedliche Materialien und erschaffen durch Partikel- oder Faserverstärkung Hochleistungsverbundwerkstoffe, die unseren Wünschen genügen. Ob wir die Struktur des Materials sehen können oder nicht, sie definiert alle Eigenschaften. Cool wäre es natürlich, wenn wir aus Kenntnis der Mikrostruktur sofort Größen für die Simulation ableiten könnten. Aber leider ist das nicht so einfach oder wissen Sie wie groß die Fließspannung bei einer Korngröße von 10 µm ist?

Glücklicherweise brauchen wir Parameter wie die Korngröße in unserer Tiefziehanalyse nicht. Allerdings verlangt Ansys Eingaben wie die Verfestigungskurve oder Orthotropiekonstanten. Wie kommen wir jetzt zu den erforderlichen Daten? Der Königsweg ist sicher, einen begnadeten Physiker zu fragen, der das Problem mit virtuoser Integralrechnung allein auf Basis der Naturkonstanten löst. Wenn man so jemanden nicht hat, ist der naheliegende und leider sehr teure Weg das Experiment: Für jede Variante der Mikrostruktur Proben herstellen und testen. Neben den hohen Kosten ist unglücklicherweise auch die Menge an durchführbaren Tests begrenzt und gewünschte Eigenschaften lassen sich gar nicht bestimmen.

Bei irdischen mathematischen und begrenzten finanziellen Möglichkeiten gibt es aber einen Ausweg: Simulation! Mittlerweile ist es weit verbreitet, FE-Modelle, sogenannte repräsentative Volumenelemente (RVEs), der Mikrostruktur zu erstellen. Der Gedanke ist bestechend: Das Verhalten der einzelnen Bestandteile wie Polyamid und Glas eines partikelverstärkten Kunststoffes lässt sich recht günstig einmalig bestimmen. Zur Beantwortung der Frage wie sich 10% oder 30% Glaskugelverstärkung auswirken, simulieren wir einfach nach Belieben Zug-, Druck-, Scherversuche in verschiedene Richtungen. Diese “synthetischen” Messdaten lassen sich nutzen, um die Verbundeigenschaften zu bestimmen. Das nennt man Homogenisierung.

Von links nach rechts: Periodische repräsentative Volumenelemente eines Kunststoffs mit 10 %, 20 % und 30 % Partikelverstärkung | © CADFEM

Wie sieht der Workflow zur Homogenisierung aus?

Am Beispiel der Partikelverstärkung soll kurz beschrieben werden, welche Schritte bei der Homogenisierung ablaufen. Der erste und mit Abstand härteste Punkt ist die Erstellung der Geometrie. RVEs werden häufig als Quader modelliert, die einen periodischen Materialausschnitt abbilden. Zunächst müssen Fragen beantwortet werden wie: welche Form sollen die Partikel haben und sind alle gleich groß oder gibt es eine Verteilungsfunktion? Dann müssen die Partikel kollisionsfrei im RVE platziert werden und das unter Beachtung des Volumenanteils und der Periodizität. Da einige Partikel von den Rändern geschnitten werden, entstehen selbst bei Kugeln komplexere geometrische Formen.

Ist die Geometrie erstellt, muss sie vernetzt werden. Natürlich will man gerne ein periodisches und an den Matrix-Partikel-Grenzflächen zusammenhängendes Netz, um Kontakte zu vermeiden. Kopfschmerzen bereiten vor allem kleine Spalte zwischen den Partikeln, die kleine Elemente erzeugen. Da ein periodisches Netz allein noch kein periodisches Ergebnis erzeugt, werden sogenannte periodische Randbedingungen aufgebracht. Dabei handelt es sich um Kopplungsgleichungen zwischen Knoten auf gegenüberliegenden Schnittflächen. Man erreicht so, dass sich auch das verformte RVE exakt periodisch aneinanderreihen lässt. Wie man an den Kanten des RVEs Overconstraints vermeidet, stellt eine beliebte Knobelaufgabe dar.

Die effektiven RVE-Dehnungen sind geschickt in die Kopplungsgleichungen integriert. An einem würfelförmigen RVE der Kantenlänge 1 µm lautet der Abstandsvektor zwischen zwei in x-Richtung gekoppelten Knoten [Δr₀]=[1 0 0] µm. Will man eine effektive RVE-Dehnung ε_xx von 2% aufbringen, wird im verformten Zustand ein Abstandsvektor von [Δr]=[1,02 0 0)] µm erzwungen. Die Periodizität drückt sich dadurch aus, dass der Abstandvektor für alle gekoppelten Knoten eines Flächenpaares gleich ist. Diese Abstandsänderungen rufen Spannungen hervor, aus denen der effektive Spannungstensor des RVEs bestimmt wird. Dieser bildet mit den effektiven RVE-Dehnungen die „synthetischen“ Messdaten zur Kalibrierung von Materialmodellen.

Periodischer Materialausschnitt und Prinzip der periodischen Randbedingungen im unverformten Zustand (links) und im verformten Zustand (rechts) | © CADFEM

Der Ansys Material Designer

Als Doktorand an der Uni habe ich den oben beschriebenen Weg zur Homogenisierung für diverse RVEs mittels Skripting umgesetzt. Mit einem lachenden und einem weinenden Auge habe ich nun sehr viel später erstmals den Ansys Material Designer geöffnet und ein kurzfaserverstärktes RVE analysiert. Dass der ganze Workflow beginnend mit der Geometrieerzeugung vollautomatisiert abläuft, hat mich sofort begeistert aber mir auch vor Augen geführt, wieviel Lebenszeit und Mühe ich vorher in diesen handwerklichen Teil investieren musste. Das ist alles Vergangenheit.

Was bleibt also zu tun? Für die Strukturmechanik muss das Materialverhalten der Einzelbestandteile wie Dichte, E-Modul und Querkontraktionszahl in den technischen Daten des Material Designers definiert werden. Natürlich muss man die maßgeblichen Mikrostrukturparameter eingeben und dann kann es nach wenigen Analyseeinstellungen schon losgehen. Wenn die Berechnungen abgeschlossen sind, kann die Material-Designer-Zelle mit den technischen Daten einer nachgeschalteten Analyse verbunden und das homogenisierte Material genutzt werden. Die Materialkarte lässt sich auch der Datenbank hinzufügen oder als xml-Datei exportieren, sodass die Homogenisierung nur einmal pro Material durchgeführt werden muss!

Für Komposite mit statistischen Eigenschaften gibt es noch eine wichtige Anmerkung: das RVE muss groß gegenüber den Fasern oder Partikeln sein und viele davon beinhalten. Prinzipiell sollte man eine Studie bezüglich der RVE-Größe machen und diese so groß wählen, dass die Eigenschaften konvergieren. Das kann sehr teuer sein, da ein RVE doppelter Kantenlänge achtmal so viele Elemente hat und der Rechenaufwand überproportional mit den Freiheitsgraden ansteigt. Der Material Designer bietet aber Abhilfe: Es können für einen Parametersatz mehrere RVEs analysiert und die Ergebnisse gemittelt werden. Dieser Aufwand steigt nur linear an und ist somit effizienter.

Ansys Workbench Workflow des Material Designers | © CADFEM

Beispiel: partikelverstärkter Kunststoff

Schauen wir uns ein Beispiel an: Wir wollen mit Glaspartikeln eine aus PA6 bestehende Matrix verstärken und der E-Modul soll sich im Vergleich zur reinen Matrix verdoppeln. Die große Preisfrage ist: Wie groß muss der Partikelanteil sein? In der Datenbank GRANTA Material Data for Simulation finden wir linear elastische Eigenschaften: E_PA6= 1100 MPa, ʋ_PA6=0,35 und E_Glas= 7000 MPa, ʋ_Glas=0,21. Der Einfachheit halber nehmen wir kugelförmige Partikel mit einer Gleichverteilung des Durchmessers zwischen 5 µm und 15 µm an. Die Größe des RVEs beträgt 30 µm. Als Zielwerte für Partikelvolumenanteile wurden 10 %, 20 % und 30 % mit jeweils 3 RVEs pro Volumenanteil analysiert.

Die Ergebnisse für die Analyse sind in der untenstehenden Tabelle zusammengefasst. Man kann erkennen, dass der Volumenanteil nicht exakt getroffen wird und die Ergebnisse eine Streuung aufweisen. Allerdings war das in Anbetracht der Größenverhältnisse auch zu erwarten. Diese Effekte werden mit größeren RVEs kleiner. Wie sind die Ergebnisse nun einzuordnen? Als Ingenieur muss ich sagen: das reicht! Da man eh kein Material mit 27,3578 % Partikelanteil bestellen kann und auch die Eingangsgrößen einer Schwankung unterliegen, ist diese Genauigkeit völlig ausreichend. Insofern wären 30 % Volumenanteil geeignet, um den E-Modul eines Verbundmaterials gegenüber der reinen Matrix zu verdoppeln.

Jenseits der Elastizität - wie geht es weiter?

Lineare Eigenschaften wie Dichte, elastische und thermische Eigenschaften bestimmt der Material-Designer komplett eigenständig. Was ist aber, wenn wir das effektive plastische Verhalten mit der Simulation selbst ermitteln wollen? Zwar bietet der Material Designer auch gewisse Möglichkeiten, nichtlineare Analysen durchzuführen, die volle Freiheit erlangen wir aber erst beim Übergang zu Ansys Mechanical. Mit einer einfachen Verlinkung auf der Projektseite können wir die periodisch vernetzte Geometrie des Material Designers einfach in Ansys Mechanical importieren. Nachdem die periodischen Randbedingungen aufgebracht wurden, können beliebige Lastsituation mit Zyklen, Haltephasen und Lastrichtungswechseln simuliert werden.

Im nachfolgenden Beispiel ist das plastische Materialverhalten eines kurzfaserverstärkten Komposits simuliert. Die Polyamidmatrix ist mit plastischem Material und isotroper Verfestigung und die Glasfasern sind elastisch modelliert. Bei anisotropen Materialien werden gerne Zugversuche in zur Faserorientierung geneigten Richtungen durchgeführt. Das kann in Ansys Mechanical sehr bequem über „Part Transform“ durchgeführt werden. Die simulierten Spannungs-Dehnungs-Kurven zeigen einen deutlichen Richtungseinfluss und können jetzt zur Kalibrierung der Hill-Plastizität genutzt werden, ganz als wären Sie im Experiment gemessen worden.

Zusammenfassend lässt sich sagen, dass der Ansys Material Designer ein starkes digitales Materiallabor darstellt. In Verbindung mit Ansys Mechanical sind der Analyse komplexer Werkstoffeigenschaften, die gar nicht oder nur sehr teuer experimentell bestimmbar sind, kaum Grenzen gesetzt. Insofern lautet mein Appell an Sie: Probieren Sie es selbst! Schnitzen Sie sich das Material, dass Ihre Bedürfnisse erfüllt.

Akkumulierte plastische Dehnung in einem kurzfaserverstärkten Kunststoff (links) bei einer effektiven Dehnung von 7 % und simulierte Spannungs-Dehnungs-Kurven bei Zugversuchen in zur Faserorientierung geneigten Richtungen (rechts) | © CADFEM

Titelbilder: Links: © CADFEM GmbH | Rechts: © Adobe Stock
Zuerst veröffentlicht: Juli 2023